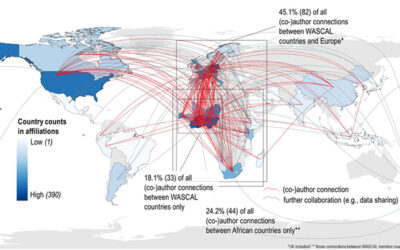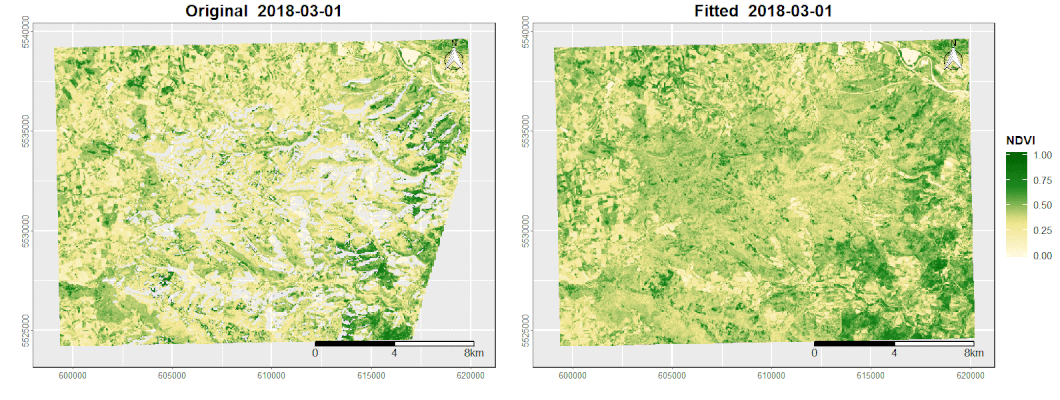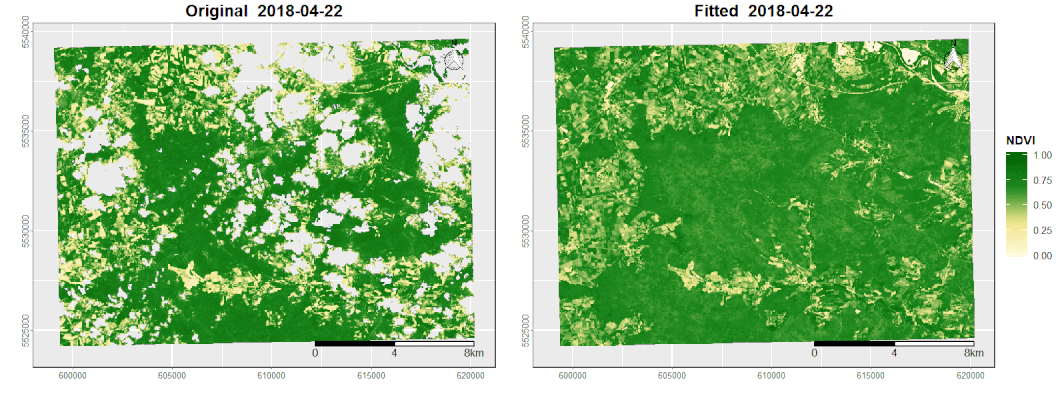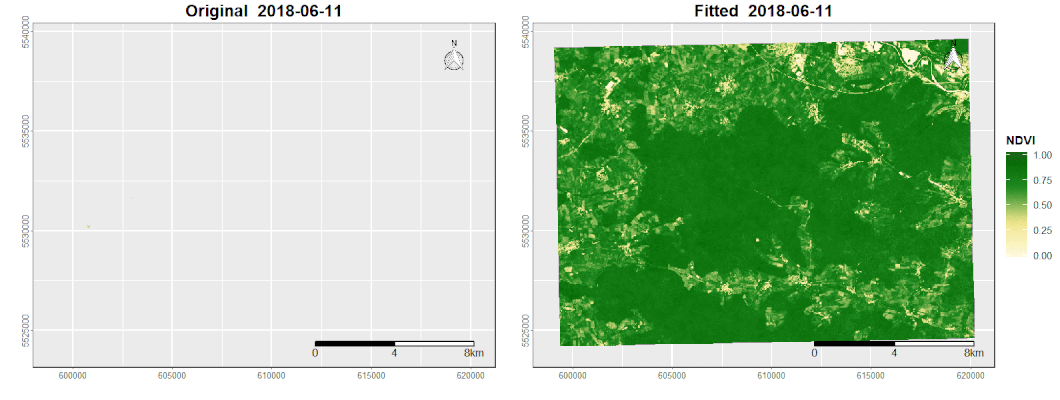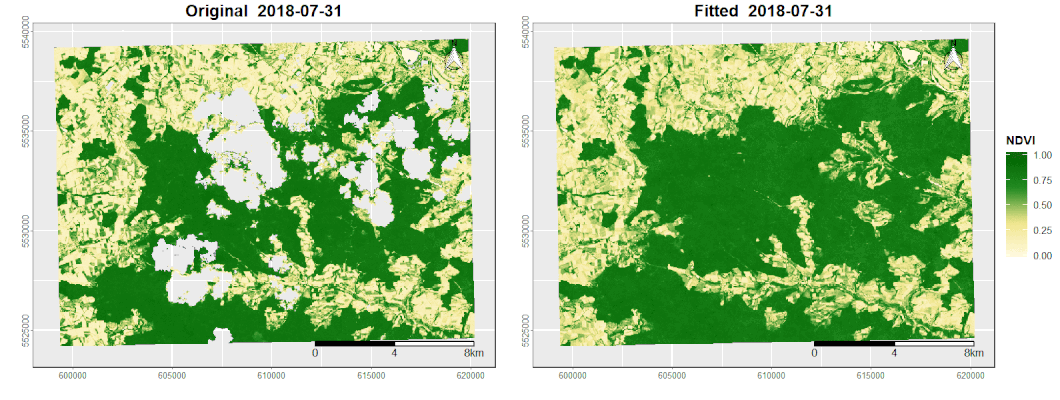
In order to fully exploit the monitoring potential of the satellite systems, challenges such as noise and data gaps must be effectively addressed. These quality losses are mainly caused by sensor artifacts, clouds, cloud shadows and other weather conditions (Verbesselt et al., 2012). In the context of time series analysis, harmonic modeling is a powerful tool to fill these gaps and reduce noise by smoothing the original signal (de Jong et al., 2011).
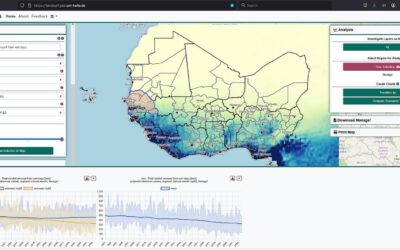
For that purpose, I created an R-package rHarmonics which enables the user to perform a harmonic analysis on a given time-series data set.
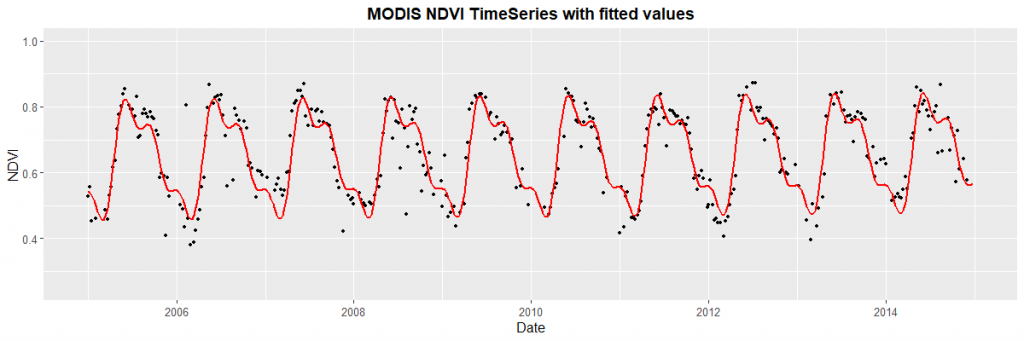
To calculate the harmonic fitted curve of a periodic signal, ordinary least squares regressions are computed using coupled sine and cosine curves on time-series data. The underlying algorithm which is based on Shumway & Stoffer (2017) equations 4.1 – 4.2 can be seen below:

Literature:
de Jong, R., de Bruin, S., de Wit, A., Schaepman, M. E., & Dent, D. L. (2011). Analysis of monotonic greening and browning trends from global ndvi time-series. Remote Sensing of Environment, 115 (2), 692–702.
Shumway, R. H., & Stoffer, D. S. (2017). Time series analysis and its applications: with r examples. Springer.
Verbesselt, J., Zeileis, A., & Herold, M. (2012). Near real-time disturbance detection using satellite image time series. Remote Sensing of Environment, 123 , 98–108.